直方体,立方体,底面が平行四辺形,ひし形の際に成り立つ公式の導出を行いました.
ポイントは,
底面積を三角形で分割,さらには分割した三角形の面積が等しい
場合に,成り立つ公式でした.
ならば,そのような条件を満たす底面の形状はほかにはないかを検討しました.
・正多角形(正六面体)
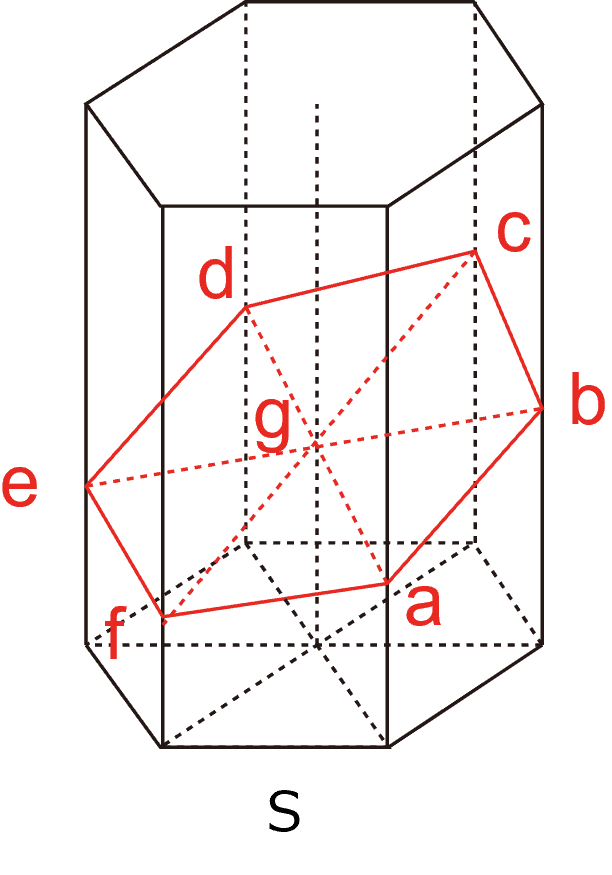
正六面体を底面に持つ立体(とりあえず,90度でそびえたつ)を斜めに切断した場合の体積です.

正六面体を取り上げたのは,できるだけシンプルで見やすいからです(正五面体でも構わないかと)
断面と側面との交点を,a, b, c, d, e, f,とします.
底面積をS,として,中心点から分割すると,6つの同じ面積を持つ三角形が出来上がります.
この断面は平面ですが,直方体と異なるのは,
立体の内側にそれぞれの三角柱の断面の交点,g,が出現する
ことです.ただ,
\( \Large \displaystyle g = \frac{a+b+c+f+e+f}{6} \)
の関係があります.各交点の高さの平均となるわけですね.
それぞれの三角柱の体積から,
\( \Large \displaystyle V = V_1 + V_2 + V_3 + V_4 + V_5 + V_6 \)
\( \Large \displaystyle= \frac{a+b+g}{3} \frac{S}{6} + \frac{b+c+g}{3} \frac{S}{6} + \frac{c+d+g}{3} \frac{S}{6}+ \frac{d+e+g}{3} \frac{S}{6}
+ \frac{e+f+g}{3} \frac{S}{6} + \frac{f+a+g}{3} \frac{S}{6}\)
\( \Large \displaystyle= \frac{S}{18} [2a + 2b+ 2c+ 2d + 2e + 2f + 6g]\)
\( \Large \displaystyle= \frac{S}{18} [3a + 3b+ 3c+ 3d + 3e + 3f ]\)
\( \Large \displaystyle= \frac{a+b+c+d+e+f}{6} S\)
となり,同様の公式を導き出すことができました.
本当にこの計算が正しいかは...ちょっと不安です.
あまり,ネットなどで正多角形に関する記載はありませんが,もし正しければ,他の正五面体,正二十面体などの立体にも適用できそうです.
次は台形を考えていきましょう